Признаки равенства треугольников

Основная идея доказательства I и II признаков равенства треугольников в учебнике Атанасяна (4) и др. Атанасян Л.С. состоит в последовательном осуществлении наложения одного из данных треугольников на другой и доказательства совмещения их при таком наложении. В доказательстве III признака существенно используется свойство углов при основании равнобедренного треугольника.

Доказательство первых двух признаков равенства треугольников в учебном пособии А.В. Погорелова и пробном учебнике А. Д. Александрова и др. Бевз Г.П. сводится к доказательству совпадения некоторого третьего треугольника, равного первому и определенным образом расположенного относительно второго, с этим вторым данным треугольником. При доказательстве первых двух признаков равенства можно использовать серию рисунков, отражающих динамику доказательства, отдельные его этапы. Так, при рассмотрении первого признака полезно использовать серию рисунков.

Рассмотрим методику изучения признаков равенства треугольников по учебнику А.В.Погорелова.

Тема: «Первый признак равенства треугольников».

Чтобы подвести к формулировке теоремы, можно в начале урока предложить учащимся следующее задание практического характера:

1) Начертите треугольник ABC.

2) Проведите луч MN и отложите от него угол KMN, равный углу ВАС. На луче МК отложите отрезок MP, равный отрезку АВ, а на луче MN - отрезок ME, равный отрезку АС.

3) Соедините точки Р и Е.

4) Измерьте и сравните отрезки ВС и РЕ, углы ABC и МРЕ, углы АСВ и МЕР.

5) Запишите равные между собой элементы построенных треугольников.

По ходу выполнения задания ставятся вопросы:

1) Сколько равных между собой углов можно отложить от данного луча?

2) Что значит «Треугольник МРЕ равен треугольнику ABC»?

3) Сформулируйте аксиому существования треугольника, равного данному, если считать данными треугольник ABC и полупрямую MN.

В результате выполнения задания на доске и в тетрадях появляется чертеж (рис.1) и запись:

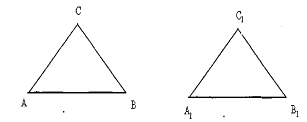
Рис. 1

По условию AB=МР, AC=МЕ, ВАС=РМЕ. Результаты измерений

АСВ=МЕР, АВС=МРЕ, ВС=РЕ.

Опираясь на определение равных треугольников, из того, что все шесть элементов одного треугольника соответственно равны мести элементам другого, делается вывод: АВС=МРЕ.

Это задание подводит учащихся к формулировке первого признака равенства треугольников.

Теорема 3.1:

(признак равенства треугольников по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство:

1. Пусть Дано: ∆АВС и ∆А2В2С2, (по аксиоме IV).

Причем расположен он может быть следующим образом: одна его вершина совпадает с вершиной А1 другая (В2) лежит на луче А1В1 a третья - (С2) лежит в той же полуплоскости относительно прямой А1В1, что и вершина С.

2. Т.к. А1В1=AB (по условию), то AB=A1B2 (из п.1), следовательно В2 совпадает с вершиной В1.

3. Т.к. B1A1C1 = BAC (по условию), то B2A1С2=BAC (из п.1), следовательно, B1A1C1 = B2A1С2

Тогда луч A1С2 совпадает с лучом A1C1.

4. AC= A1C1 (по условию), A1С2=AC (из п.1), следовательно A1C1= A1С2. Тогда вершина С2 совпадет с вершиной С1.

Таким образом, ∆АВС = ∆А1В1С1

Ч.т.д.

После доказательства теоремы о первом признаке равенства треугольников предлагаются задачи:

Задача 1.В каждой из изображенных на рисунке пар треугольников равные элементы треугольников указаны пометками. Какие треугольники равны по первому признаку?

Статьи по теме:

Дидактические игры
В отличие от других видов деятельности игра содержит цель в самой себе; посторонних и отдаленных задач в игре ребенок не ставит и не решает. Игра часто и определяется как деятельность, которая выполн ...

Виды изложений и их классификация
В школьной практике используются разные по цели и разнообразные по содержанию исходного текста изложения. По цели это изложения контрольные и обучающие. Основное различие между ними в том, что перед ...

Сенсомоторное развитие дошкольников
Прежде чем раскрыть значение сенсомоторного развития для детей старшего дошкольного возраста нам необходимо рассмотреть, что собой представляет сенсорное и моторное развитие детей. Сенсорное развитие ...

Навигация

• Главная
• Тенденции современной педагогики
• Спортивно-педагогическая деятельность
• Социализация подростка
• Стандартизация в системе образования
• Связь педагогики с другими науками
• Профессиональное обучение
• Статьи о педагогике