Методика изучения темы «Прямоугольник»

Далее вводится понятия «равнобедренная трапеция» и «средняя линия трапеции», и рассматривается теорема 6.8 (о средней линии трапеции): «Средняя линия трапеции параллельна основаниям и равна их полусумме».

В учебнике «Геометрия 7-9» Л.С. Атанасяна (4) понятие «трапеция» вводится в §2 «Параллелограмм и трапеция» в пункте 44 «Трапеция»:

«Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны - боковыми сторонами.

Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной».

Рассмотрим методику изучения темы «Трапеция» на примере учебника А.В. Погорелова.

Трапецией называется четырехугольник, у которого только две противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами.

На рисунке вы видите трапецию ABCD с основаниями АВ и CD и боковыми сторонами ВС и AD.

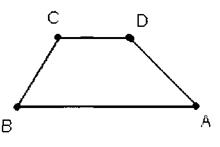
Трапеция, у которой боковые стороны равны, называется равнобокой. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Теорема 6.8: Средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD-трапеция,

QP-средняя линия.

Доказать: QР||ВС,

QP||AD,

QP=½ (BC+AD).

Доказательство.

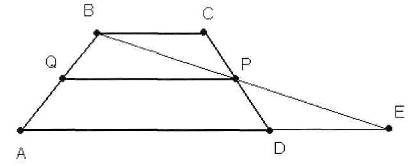
BP⋂AD=E, ∆PBC=∆PED (по второму признаку равенства треугольников) CP=DP (по построению), PCB=PDE (внутренние накрест лежащие при параллельных прямых ВС и AD и секущей CD),BPC=EPD (вертикальные).

Из равенства треугольников => РВ=РЕ, BC=ED.

Значит средняя линия PQ трапеции является средней линией ∆АВЕ. По свойству сред, линии треугольника PQ||AE и отрезок

pq = ½АЕ= ½(ad+bc).

Ч.т.д.

После введения выше перечисленных понятий школьники решают задачи.

Задача1.

В

трапеции ABCD углы, прилежащие к стороне AD, равны 74 и 81. Определите углы прилежащие к стороне ВС. (устно).

Ответ: ABC=106, BCD=99.

Задача2.

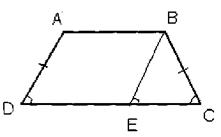
Докажите, что у равнобокой трапеции углы при основании равны.

Дано: ABCD-равнобокая трапеция,

АВ, CD-основания.

Доказать: A=B, D=C.

Доказательство.

BP||AD, ABED - параллелограмм => BE=AD (по свойству параллелограмма) AD=BC (по условию) => ∆ВСЕ - равнобедренный с основанием ЕС. Углы треугольника и трапеции при вершине С совпадают, а углы при вершине Е и D равны как соответственные углы при пересечении параллельных прямых секущей. Поэтому ADC=BCD.

Статьи по теме:

Общая характеристика муниципального дошкольного образовательного учреждения детский сад №35 г. Челябинска
Муниципальное дошкольное образовательное учреждение Детский сад присмотра и оздоровления с приоритетным осуществлением санитарно-гигиенических, профилактических и оздоровительных мероприятий и процед ...

Понятия взаимодействия, сотрудничества
взаимодействие сотрудничество педагог дошкольный Сегодня, признав приоритет семейного воспитания перед общественным, возложив ответственность за воспитание детей на родителей мы понимаем, что это тре ...

Апробация виртуальной лаборатории «Открытая физика»
Апробация разработанных учебно-методических материалов в поддержку уроков по теме «Электричество и магнетизм» на основе использования мультимедийного курса «Открытая физика» проходила в 10-ом классе ...

Навигация

• Главная
• Тенденции современной педагогики
• Спортивно-педагогическая деятельность
• Социализация подростка
• Стандартизация в системе образования
• Связь педагогики с другими науками
• Профессиональное обучение
• Статьи о педагогике