Методика изучения темы «Прямоугольник»

В учебнике «Геометрия 7-11» А.В. Погорелова понятие «прямоугольник» вводится в §6 «Четырехугольники» в пункте 54 «Прямоугольник»: Прямоугольник - это параллелограмм, у которого все углы прямые.

В учебнике «Геометрия 7-9» Л.С. Атанасяна тема «Прямоугольник рассматривается в §3 «Прямоугольник, ромб, квадрат» в п.45 «Прямоугольник»: в начале параграфа вводится определение: «прямоугольником называется параллелограмм, у которого все углы прямые», а затем рассматривают свойство прямоугольника (диагонали прямоугольника равны) и признак прямоугольника (если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник).

Рассмотрим методику изучения темы «Прямоугольник» на примере учебника А.В. Погорелова.

Прямоугольник - это параллелограмм, у которого все углы прямые.

Для изучения свойства прямоугольника, классу можно предложить вопросы:

1. Равны ли диагонали у произвольного параллелограмма? (на доске нарисован параллелограмм, не являющийся прямоугольником).

2. Равны ли диагонали у прямоугольника?

3. Докажите равенство диагоналей прямоугольника ABCD, рассмотрев треугольники BAD и CDA.

4. Сформулируйте теорему о свойствах прямоугольника.

Теорема 6.4.

Диагонали прямоугольника равны.

После введения определения и свойства прямоугольника школьники решают задачи.

Задача 1

. Докажите, что если у параллелограмма все углы равны, то он является прямоугольником.

Дано: ABCD-параллелограмм,

A=B=С=D.

Доказать: ABCD-прямоугольник.

Доказательство.

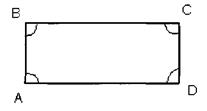
A+B=180, т.к. они являются внутренними односторонними при параллельных прямых ВС и AD и секущей АВ. => A=B=90.

=> ABCD - прямоугольник.

Задача 2.

В параллелограмме из вершин углов на противолежащие стороны опущены перпендикуляры. Докажите, что полученный четырехугольник - прямоугольник.

Дано: GBFD-параллелограмм,

BAGD,DCBF.

Доказать: ABCD-прямоугольник.

Доказательство.

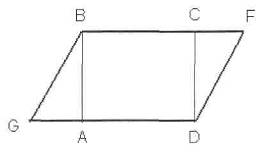
BC||AD, так как GBFD - параллелограмм;

BAD=90, так как BAGD.

АВС=90, так как BAD и ABC— внутренние односторонние углы при BF||GD и секущей АВ.

BCD=90, так как DCBF.

CAD=90, так как CAD и BCD - внутренние односторонние углы при BF||GD и секущей DC.

Статьи по теме:

Организационные процессы
Система управления в организации, ход властных и информационных потоков. Высшим должностным лицом МОУ СОШ № 10 является директор. Он принимает решения, которые разрабатываются совместно с Управленчес ...

Программа практикума «Диагностика физического развития детей» и технология руководства самостоятельной деятельностью студентов при его реализации
Пояснительная записка. Практикум «Диагностика физического развития детей» направлен на формирование самостоятельной работы студентов среднего специального учебного заведения. Включение данного практи ...

Развитие технического творчества учащихся
Развитие технического творчества учащихся можно применять совершенно с другой целью, чем это требуется по условию. Здесь важно иметь в виду, что деятельность учащихся, их конкретные действия, характе ...

Навигация

• Главная
• Тенденции современной педагогики
• Спортивно-педагогическая деятельность
• Социализация подростка
• Стандартизация в системе образования
• Связь педагогики с другими науками
• Профессиональное обучение
• Статьи о педагогике